What is a Function?
A function relates an input to an output.
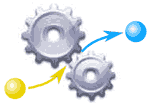 |
It is like a machine that has an input and an output. And the output is related somehow to the input. |
| f(x) | "f(x) = ... " is the classic way of writing a function. And there are other ways, as you will see! |
Input, Relationship, Output
We will see many ways to think about functions, but there are always three main parts:- The input
- The relationship
- The output
Example: "Multiply by 2" is a very simple function.
Here are the three parts:| Input | Relationship | Output |
|---|---|---|
| 0 | × 2 | 0 |
| 1 | × 2 | 2 |
| 7 | × 2 | 14 |
| 10 | × 2 | 20 |
| ... | ... | ... |
Some Examples of Functions
- x2 (squaring) is a function
- x3+1 is also a function
- Sine, Cosine and Tangent are functions used in trigonometry
- and there are lots more!
... instead we will look at the general idea of a function.
Names
First, it is useful to give a function a name.The most common name is "f", but we can have other names like "g" ... or even "marmalade" if we want.
But let's use "f":

We say "f of x equals x squared"
what goes into the function is put inside parentheses () after the name of the function:
So f(x) shows us the function is called "f", and "x" goes in
And we usually see what a function does with the input:
f(x) = x2 shows us that function "f" takes "x" and squares it.
Example: with f(x) = x2:
- an input of 4
- becomes an output of 16.
In fact we can write f(4) = 16.
The "x" is Just a Place-Holder!
Don't get too concerned about "x", it is just there to show us where the input goes and what happens to it.It could be anything!
So this function:
f(x) = 1 - x + x2
Is the same function as:- f(q) = 1 - q + q2
- h(A) = 1 - A + A2
- w(θ) = 1 - θ + θ2
f(2) = 1 - 2 + 22 = 3
Sometimes There is No Function Name
Sometimes a function has no name, and we see something like:
y = x2
But there is still:- an input (x)
- a relationship (squaring)
- and an output (y)
Relating
At the top we said that a function was like a machine. But a function doesn't really have belts or cogs or any moving parts - and it doesn't actually destroy what we put into it!
A function relates an input to an output.
Saying "f(4) = 16" is like saying 4 is somehow related to 16. Or 4 → 16
h(age) = age × 20
So, if the age is 10 years, the height is:
h(10) = 10 × 20 = 200 cm
Here are some example values:| age | h(age) = age × 20 |
|---|---|
| 0 | 0 |
| 1 | 20 |
| 3.2 | 64 |
| 15 | 300 |
| ... | ... |
What Types of Things Do Functions Process?
"Numbers" seems an obvious answer, but ...
|
... which numbers? For example, the tree-height function h(age) = age×20 makes no sense for an age less than zero. |
|
| ... it could also be letters ("A"→"B"), or ID codes ("A6309"→"Pass") or stranger things. | |
|
A set is a collection of things.Here are some examples:
Set of even numbers: {..., -4, -2, 0, 2, 4, ...}
Set of clothes: {"hat","shirt",...} Set of prime numbers: {2, 3, 5, 7, 11, 13, 17, ...} Positive multiples of 3 that are less than 10: {3, 6, 9} |
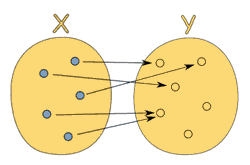
So, a function takes elements of a set, and gives back elements of a set.
A Function is Special
But a function has special rules:- It must work for every possible input value
- And it has only one relationship for each input value
 |
Formal Definition of a Function
A function relates each element of a set
with exactly one element of another set (possibly the same set). |
The Two Important Things!
1.
|
"...each element..." means that every element in X is related to some element in Y. We say that the function covers X (relates every element of it). (But some elements of Y might not be related to at all, which is fine.) |
2.
|
"...exactly one..." means that a function is single valued. It will not give back 2 or more results for the same input.
So "f(2) = 7 or 9" is not right!
|
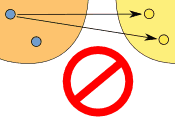
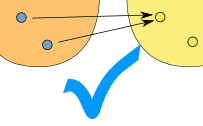
| Note: "One-to-many" is not allowed, but "many-to-one" is allowed: | ||
 |
 |
|
| (one-to-many) | (many-to-one) | |
| This is NOT OK in a function | But this is OK in a function | |
Example: The relationship x → x2
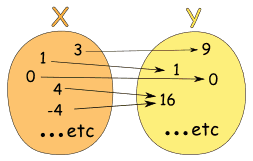
Could also be written as a table:
| X: x | Y: x2 |
|---|---|
| 3 | 9 |
| 1 | 1 |
| 0 | 0 |
| 4 | 16 |
| -4 | 16 |
| ... | ... |
It is a function, because:
- Every element in X is related to Y
- No element in X has two or more relationships
(Notice how both 4 and -4 relate to 16, which is allowed.)
Example: This relationship is not a function:
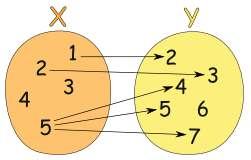
- Value "3" in X has no relation in Y
- Value "4" in X has no relation in Y
- Value "5" is related to more than one value in Y
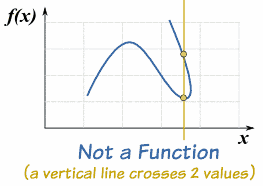 |
Vertical Line TestOn a graph, the idea of single valued means that no vertical line ever crosses more than one value.If it crosses more than once it is still a valid curve, but is not a function. |
Some types of functions have stricter rules, to find out more you can read Injective, Surjective and Bijective
Infinitely Many
My examples have just a few values, but functions usually work on sets with infinitely many elements.Example: y = x3
- The input set "X" is all Real Numbers
- The output set "Y" is also all the Real Numbers
| X: x | Y: x3 |
|---|---|
| -2 | -8 |
| -0.1 | -0.001 |
| 0 | 0 |
| 1.1 | 1.331 |
| 3 | 27 |
| and so on... | and so on... |
Domain, Codomain and Range
In our examples above- the set "X" is called the Domain,
- the set "Y" is called the Codomain, and
- the set of elements that get pointed to in Y (the actual values produced by the function) is called the Range.
So Many Names!
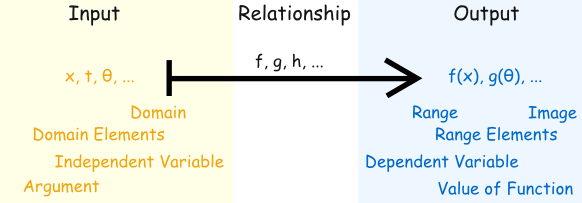
Functions have been used in mathematics for a very long time, and lots of different names and ways of writing functions have come about.Here are some common terms you should get familiar with:
Example: with z = 2u3:
- "u" could be called the "independent variable"
- "z" could be called the "dependent variable" (it depends on the value of u)
Example: with f(4) = 16:
- "4" could be called the "argument"
- "16" could be called the "value of the function"
Ordered Pairs
And here is another way to think about functions:
Write the input and output of a function as an "ordered pair", such as (4,16).
They are called ordered pairs because the input always comes first, and the output second:
(input, output)
So it looks like this:
( x, f(x) )
Example:
(4,16) means that the function takes in "4" and gives out "16"
Set of Ordered Pairs
A function can then be defined as a set of ordered pairs:
Example: {(2,4), (3,5), (7,3)} is a function that says
But the function has to be single valued, so we also say
"2 is related to 4", "3 is related to 5" and "7 is related 3".
Also, notice that:- the domain is {2,3,7} (the input values)
- and the range is {4,5,3} (the output values)
"if it contains (a, b) and (a, c), then b must equal c"
Which is just a way of saying that an input of "a" cannot produce two different results.
Example: {(2,4), (2,5), (7,3)} is not a function because {2,4} and {2,5} means that 2 could be related to 4 or 5.
In other words it is not a function because it is not single valued
In other words it is not a function because it is not single valued
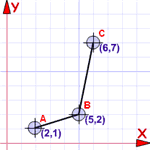 |
A Benefit of Ordered PairsWe can graph them...... because they are also coordinates! So a set of coordinates is also a function (if they follow the rules above, that is) |
A Function Can be in Pieces
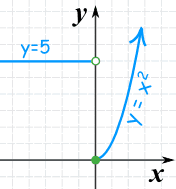
We can create functions that behave differently depending on the input valueExample: A function with two pieces:
- when x is less than 0, it gives 5,
- when x is 0 or more it gives x2
 |
Here are some example values:
|
Explicit vs Implicit
One last topic: the terms "explicit" and "implicit"."Explicit" is when the function shows us how to go directly from x to y, such as:
y = x3 - 3
When we know x, we can find y
"Implicit" is when it is not given directly such as:
x2 - 3xy + y3 = 0
When we know x, how do we find y?