Quadratic Equations

Name

The name Quadratic comes from "quad" meaning square, because the variable gets squared (like x²).
It is also called an "Equation of Degree 2" (because of the "2" on the x)

Standard Form

The Standard Form of a Quadratic Equation looks like this:

a, b and c are known values. a can't be 0. "x" is the variable or unknown (we don't know it yet).

Here are some more examples:

2x2 + 5x + 3 = 0		In this one a=2, b=5 and c=3
x2 − 3x = 0		This one is a little more tricky: Where is a? Well a=1, and we don't usually write "1x2" b = -3 And where is c? Well c=0, so is not shown.
5x − 3 = 0		Oops! This one is not a quadratic equation: it is missing x2 (in other words a=0, which means it can't be quadratic)

Hidden Quadratic Equations!

So the "Standard Form" of a Quadratic Equation is

ax² + bx + c = 0

But sometimes a quadratic equation doesn't look like that! For example:

In disguise	→	In Standard Form	a, b and c
x2 = 3x -1	Move all terms to left hand side	x2 - 3x + 1 = 0	a=1, b=-3, c=1
2(w2 - 2w) = 5	Expand (undo the brackets), and move 5 to left	2w2 - 4w - 5 = 0	a=2, b=-4, c=-5
z(z-1) = 3	Expand, and move 3 to left	z2 - z - 3 = 0	a=1, b=-1, c=-3
5 + 1/x - 1/x2 = 0	Multiply by x2	5x2 + x - 1 = 0	a=5, b=1, c=-1

Have a Play With It Play with the "Quadratic Equation Explorer" so you can see: the graph it makes, and the solutions (called "roots").

How To Solve It?

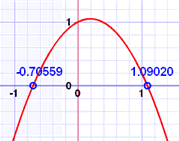
The "solutions" to the Quadratic Equation are where it is equal to zero.
There are usually 2 solutions (as shown in the graph above).
They are also called "roots", or sometimes "zeros"

There are 3 ways to find the solutions:

1. We can Factor the Quadratic (find what to multiply to make the Quadratic Equation)

2. We can Complete the Square, or

3. We can use the special Quadratic Formula:

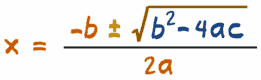
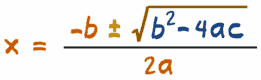
Just plug in the values of a, b and c, and do the calculations.

We will look at this method in more detail now.

.

Discriminant

Do you see b² - 4ac in the formula above? It is called the Discriminant, because it can "discriminate" between the possible types of answer:

when b² - 4ac is positive, we get two Real solutions
when it is zero we get just ONE real solution (both answers are the same)
when it is negative we get two Complex solutions

Complex solutions? Let's talk about them after we see how to use the formula.

Example: Solve 5x² + 6x + 1 = 0

Coefficients are:		a = 5, b = 6, c = 1
Quadratic Formula:		x = [ −b ± √(b2 − 4ac) ] / 2a
Put in a, b and c:		x = [ −6 ± √(62 − 4×5×1) ] / (2×5)
Solve:		x = [ −6 ± √(36−20) ]/10
		x = [ −6 ± √(16) ]/10
		x = ( −6 ± 4 )/10
		x = −0.2 or −1

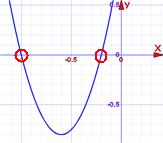Answer: x = -0.2 or x = -1 And we see them on this graph.

Check -0.2:	5×(-0.2)² + 6×(-0.2) + 1 = 5×(0.04) + 6×(-0.2) + 1 = 0.2 -1.2 + 1 = 0
Check -1:	5×(-1)² + 6×(-1) + 1 = 5×(1) + 6×(-1) + 1 = 5 - 6 + 1 = 0

Complex Solutions?

When the Discriminant (the value b² - 4ac) is negative we get Complex solutions ... what does that mean?
It means our answer will include Imaginary Numbers. Wow!

Example: Solve 5x² + 2x + 1 = 0

Coefficients are:		a = 5, b = 2, c = 1
Note that The Discriminant is negative:		b2 - 4ac = 22 - 4×5×1 = -16
Use the Quadratic Formula:		x = [ -2 ± √(-16) ] / 10
The square root of -16 is 4i (i is √-1, read Imaginary Numbers to find out more)
So:		x = ( -2 ± 4i )/10

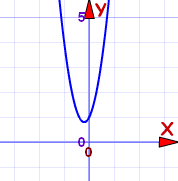Answer: x = -0.2 ± 0.4i The graph does not cross the x-axis. That is why we ended up with complex numbers.

In some ways it is easier: we don't need more calculation, just leave it as -0.2 ± 0.4i.