What is Trigonometry

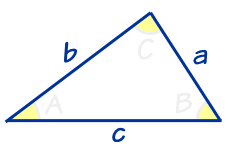
Trigonometry ... is all about triangles.

Right Angled Triangle

The triangle of most interest is the right-angled triangle.
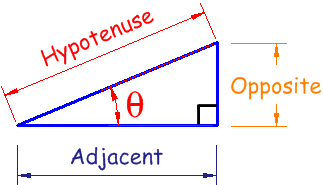
The right angle is shown by the little box in the corner.
We usually know another angle θ.
And we give names to each side:

• Adjacent is adjacent (next to) to the angle θ
• Opposite is opposite the angle θ
• the longest side is the Hypotenuse

"Sine, Cosine and Tangent"

Trigonometry is good at find a missing side or angle in a triangle.
The special functions Sine, Cosine and Tangenthelp us!

They are simply one side of a right-angled triangle divided by another.

For any angle "θ":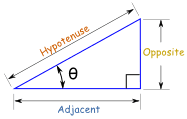

Sine Function:	sin(θ) = Opposite / Hypotenuse
Cosine Function:	cos(θ) = Adjacent / Hypotenuse
Tangent Function:	tan(θ) = Opposite / Adjacent

(Sine, Cosine and Tangent are often abbreviated to sin, cos and tan.)

Example: What is the sine of 35°?

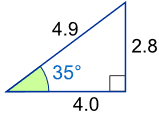Using this triangle (lengths are only to one decimal place): sin(35°) = Opposite / Hypotenuse = 2.8/4.9 = 0.57...

Calculators have sin, cos and tan, let's see how to use them:

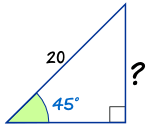
Example: What is the missing length here?

• We know the Hypotenuse
• We want to know the Opposite

Sine is the ratio of Opposite / Hypotenuse

Get a calculator, type in "45", then the "sin" key:

sin(45°) = 0.7071...

Now multiply by 20 (the Hypotenuse length):

Opposite length = 20 × 0.7071... = 14.14 (to 2 decimals)

Try Sin Cos and Tan!

Move the mouse around to see how different angles affect sine, cosine and tangent:
And you will also see why trigonometry is also about circles! In this animation the hypotenuse is 1, making the Unit Circle.
Notice that the sides can be positive or negative according to the rules of Cartesian coordinates. This makes the sine, cosine and tangent change between positive and negative also.

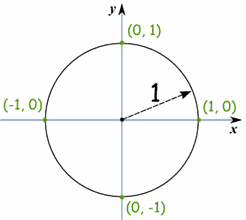
Unit Circle

What you just played with is the Unit Circle.
It is a circle with a radius of 1 with its center at 0.
Because the radius is 1, we can directly measure sine, cosine and tangent.
Here we see the sine function being made by the unit circle:







You can also see the nice graphs made by sine, cosine and tangent.

Degrees and Radians

Angles can be in Degrees or Radians. Here are some examples:

Angle	Degrees	Radians
Right Angle	90°	π/2
__ Straight Angle	180°	π
Full Rotation	360°	2π

Repeating Pattern

Because the angle is rotating around and around the circle the Sine, Cosine and Tangent functions repeat once every full rotation (see Amplitude, Period, Phase Shift and Frequency).
When we need to calculate the function for an angle larger than a full rotation of 2π (360°) we subtract as many full rotations as needed to bring it back below 2π (360°):

Example: what is the cosine of 370°?

370° is greater than 360° so let us subtract 360°

370° − 360° = 10°

cos(370°) = cos(10°) = 0.985 (to 3 decimal places)

And when the angle is less than zero, just add full rotations.

Example: what is the sine of −3 radians?

−3 is less than 0 so let us add 2π radians

−3 + 2π = −3 + 6.283 = 3.283 radians

sin(−3) = sin(3.283) = −0.141 (to 3 decimal places)

Solving Triangles

A big part of Trigonometry is Solving Triangles. "Solving" means finding missing sides and angles.

Example: Find the Missing Angle "C"

Angle C can be found using angles of a triangle add to 180°:

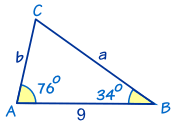
So C = 180° − 76° − 34° = 70°

It is also possible to find missing side lengths and more. The general rule is:

When we know any 3 of the sides or angles we can find the other 3
(except for the three angles case)

See Solving Triangles for more details.

Other Functions (Cotangent, Secant, Cosecant)

Similar to Sine, Cosine and Tangent, there are three other trigonometric functions which are made by dividing one side by another:

Cosecant Function:	csc(θ) = Hypotenuse / Opposite
Secant Function:	sec(θ) = Hypotenuse / Adjacent
Cotangent Function:	cot(θ) = Adjacent / Opposite

Trigonometric and Triangle Identities

And as you get better at Trigonometry you can learn these: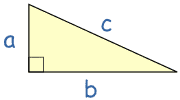

	The Trigonometric Identities are equations that are true for all right-angled triangles.
	The Triangle Identities are equations that are true for all triangles (they don't have to have a right angle).